MC6800のプログラミングテクニック(21) 除算の再検討・データの性質
整数除算の商のビットの0,1を数えると、0になるビットが多く １は少ない。その性質が整数除算の高速化に使える。
被除数（a）と除数（d）がランダムに分布していると仮定してみよう（実際には扱うデータによって異なるはずだが、簡単に考えてみる）。
ビット幅をnとすれば、以下の性質は自明である。0が多いのは明らか。
- d>a であれば、d=0 である （ビットは全て0）。
- 全ビットが立つのは a=2n-1、d=1のときに限る。
- dが2m程度の数であれば、少なくとも商の上位 n-m bitはゼロになる。
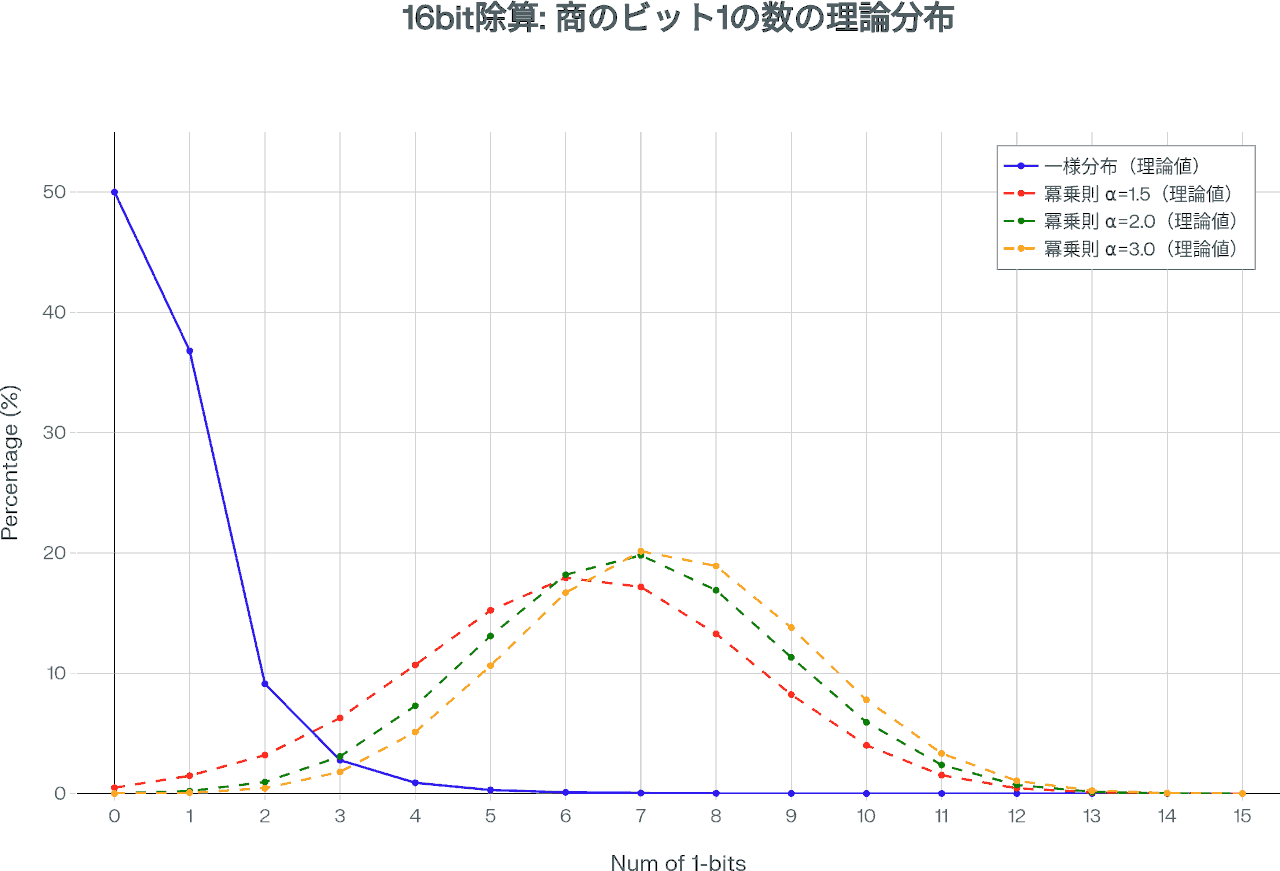
bit1の割合グラフ
除数・被除数をランダムにすると、商が全て0になるパターンが半分程度を占める。
被除数<除数である場合は、商が0になるので当然である。
もっとも実際の計算では、除数は比較的小さな数が多いはずなので、ここまで0は多くならない。
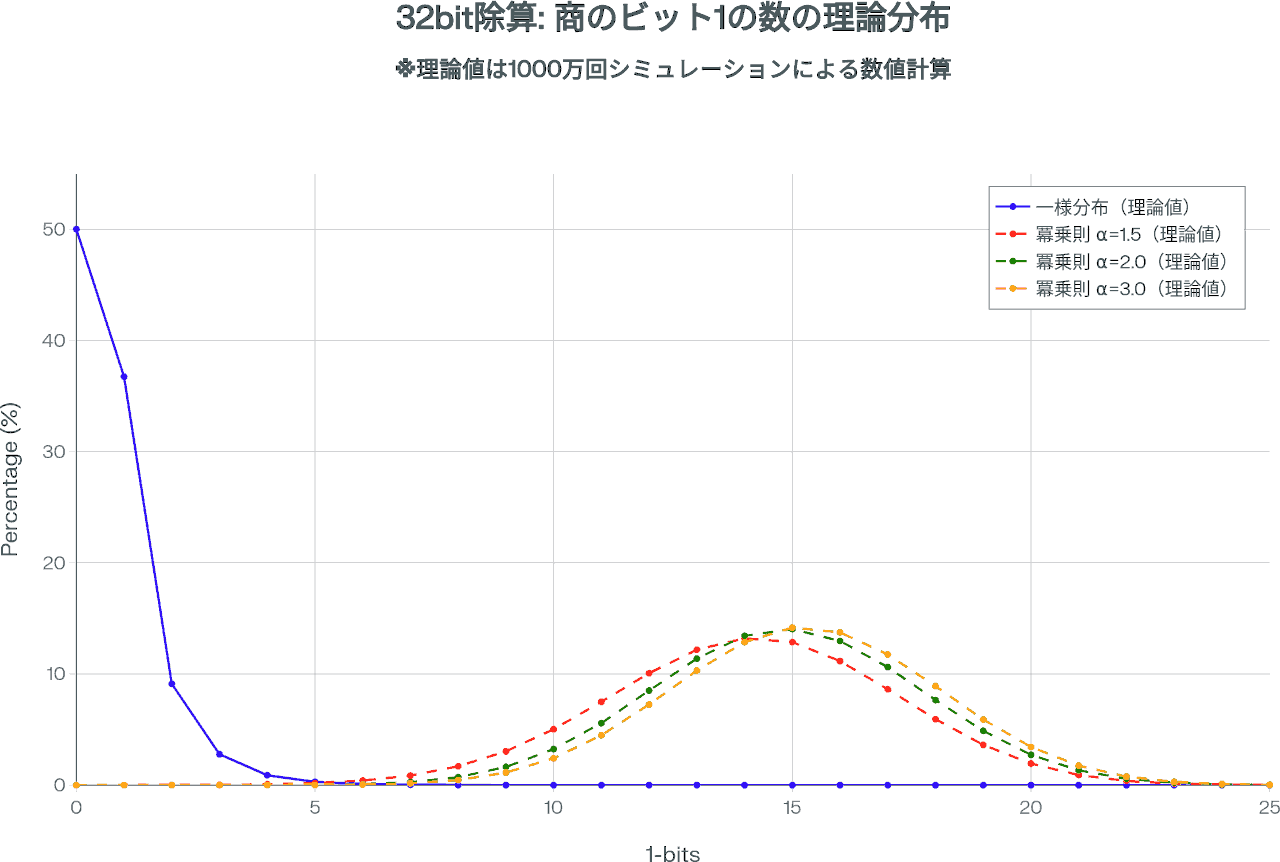
除数・被除数がランダムな場合と、被除数はランダム・除数は冪乗則に従う場合に 商の1になるbitの数は下のグラフのように分布する。
小さい除数が増えるほど（αが大きくなるほど）、商に占める 1の割合は増えるが、どの場合でも0の方が多い。
このグラフは被除数がランダムに分布していると仮定しているが、もし被除数も小さい方に偏っている場合は さらに 0のbitが増える。
なお、除数が2nの形の場合はコンパイラがシフト演算に最適化するので、1,2,4,8などは除算ルーチンを通らない。これも0を増やす方向に働く。
0の方を高速化すべき（回復法より比較法）
8bit除算の項で述べたが、一般的に除算で使われている回復法では、引けなかった時（商に0が立つ時）に、除数を足して回復処理を行う。そのため、0のときに遅くなる。
8bit処理では比較して引けるときに（商が1のときだけ）、除数を引き算するのが良い。
MC6800には16bit比較命令がないので 比較法を使うとpsh/pulが追加で必要になる。比較法でなく、回復法か非回復法を使うべき。
MC6809など後継のCPUなら CMPD命令があるので比較法でも良さそう（CMPDはADDD/SUBDよりも1cyc遅いので微妙か？）。
32bitの場合は 使えるレジスタが足りないので、どのみちAccABをpsh/pulする必要がある。回復法でも比較法でもコストは変わらないので、比較法の方が早い。