MC6800のプログラミングテクニック(25) 除算の再検討 電大版TinyBASICの除算
除算の再検討のために、過去に発表されたプログラムの除算を見ていたら、あれ？と思う部分があった。
Nakamozu Tiny BASIC と 電大版Tiny BASICである。前者は後者を参考にしたと思われるので、電大版を見てみよう。
電大版Tiny BASICの除算ルーチンのメインループ部分は以下の通りである。
シフトしながら引いてみて、ダメなら足すという回復法（引き戻し法）の除算である。でも なんか変だ。
（電大版ではAccBが上位、AccBを下位にしているので そこも気になるけど、問題はそこではない）
BINDIV BSR SETCNT DIV2 BSR ROL2X ROLA ROLB SUBA 1,X SBCB 0,X BSR CHECK DIV3 DEC F BNE DIV2 ROL2X ROL 3,X ROL 2,X RTS * CHECK PSHB EORB 0,X PULB SEC BPL *+7 ADDA 1,X ADCB 0,X CLC RTS
通常の引き戻し法との違い
通常の引き戻し法では、引けなかったら（キャリーが出たら）足して元に戻すのだが、その部分が CHECK というサブルーチンになっている。
サブルーチン先頭で、剰余と除数をXORして、その符号を見ている。符号が同一ならC=1にして戻り、違っている場合は回復してC=0にしている。
なんだこれは？
符号の調整もしていない
私の作り方だと除算ルーチンは無符号で作っておいて、2の補数の場合は符号を調整するための前処理・後処理を入れるようにしている。
電大版でも前処理・後処理はあるけど、符号の調整ではなさそうである。これはなんだ？
DIVIDE LDAA 0,X ORAA 1,X BEQ ERR140 BSR SETCNT BSR ROL2X ROLA NEGA TAB BSR CHECK ROLA EORA #1 ROLA BSR DIV3 JSR CMPX BNE RDIV CLRA TAB INC 3,X BNE *+4 INC 2,X RDIV INX INX RTS
最初に被除数の最上位ビットを見て、1（負）なら剰余の初期値を-1にしている。
その上で引き算処理をしてから、メインループに入る。
後処理としてAccBAと0-1,Xを比較（CMPX）して、その結果を見て商に1を足している。
負数も扱える回復法除算
結局、このルーチンは負数も扱える回復法除算だった。
通常の正数のみの回復法では、引いてみてキャリーが出たら戻す。
しかし除数が負の場合を考えると、単純にキャリーを見たのではダメで、引いた結果の符号が除数と同じかどうかを見ないといけない。
CHECKルーチンがその判定を行っていて、AccB （剰余の上位バイト）と 0,X （除数の上位バイト）の XOR をとって符号が同じかどうかを判定している。
CHECK PSHB EORB 0,X PULB SEC BPL *+7
後処理では 剰余==除数になった場合に、商を +1 している。
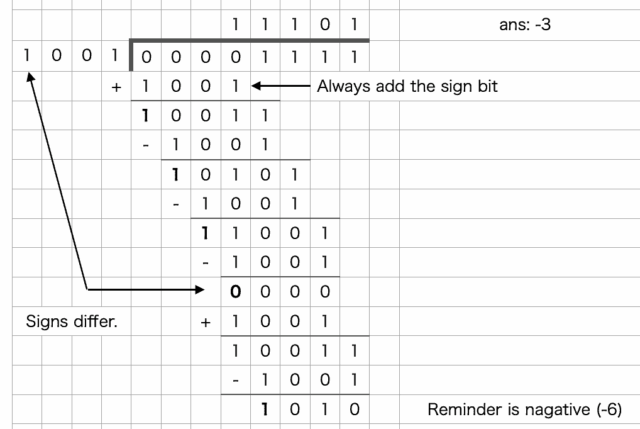
15 ➗ -7 = -3 余り -6 となる。CではなくPythonのような除算だ。
アルゴリズムの詳細
このアルゴリズムは、1978年8月発行のマイクロコンピュータプログラミング入門 : Tiny BASIC インタプリタにも掲載されている方法と同一だ。著者は石田晴久先生。序文に「乗除算ルーチンの構成法を教示していただいた和田英一教授（東大計数工学科）」とある。
本書の 「3.5.3 2進法のわりざん」に解説がある。それには下記のように書かれていて、符号の判定が厄介なので負数が使えるようにしたようだ。
2進数のわりざんにはいろいろなやり方がある。B÷Dの形のわりざんをするのに、もっとも常識的なのは、符号を別に考えて，|B|÷|D|のわりざんを行って、商を求める方法である。しかしこれでは、次の例のように商および余りの符号をきめるのが厄介である。
そして、前処理・後処理の方法についても詳しく解説されている。
しかし、符号の判定のコストよりも負数を扱っているコストの方が大きいように思える。
少なくとも速度は正数+符号補正の方が早い。バイト数は補正のコスト次第。
この方法では剰余は除数と同じ符号になるし、商は負に向かって切り捨てられる（floor）。そのため、符号の処理に加えて剰余を見て商の補正が必要になる。
たしかに厄介ではある。